mod_solver Module Reference

This module contains subroutines to compute Newmark explicit time marching scheme, external forces \( F^{ext} \), internal forces \( KU \) and boundary traction forces \( C\dot{U} \) of the system \( M\ddot{U} + C\dot{U} + KU = F^{ext} \).

Public Member Functions
subroutine, public	newmark_ini ()
	This subroutine initializes Newmark time marching scheme at step n+1. More...
subroutine, public	newmark_end ()
	This subroutine finalizes Newmark time marching scheme at step n+1. More...
subroutine, public	compute_internal_forces_order4 (elt_start, elt_end)
	This subroutine computes internal forces \( \int _{\Omega} \boldsymbol{\epsilon}(\mathbf{v}) ^{T} \colon \boldsymbol{\tau} \, d\Omega \) for spectral-elements of order 4. Stress-strain relationship can be linear elastic (general isotropic fourth-order Hooke's law for continuous media) or viscoelastic (memory variables method). More...
subroutine, public	compute_internal_forces_order5 (elt_start, elt_end)
	This subroutine computes internal forces \( \int _{\Omega} \boldsymbol{\epsilon}(\mathbf{v}) ^{T} \colon \boldsymbol{\tau} \, d\Omega \) for spectral-elements of order 5. Stress-strain relationship can be linear elastic (general isotropic fourth-order Hooke's law for continuous media) or viscoelastic (memory variables method). More...
subroutine, public	compute_internal_forces_order6 (elt_start, elt_end)
	This subroutine computes internal forces \( \int _{\Omega} \boldsymbol{\epsilon}(\mathbf{v}) ^{T} \colon \boldsymbol{\tau} \, d\Omega \) for spectral-elements of order 6. Stress-strain relationship can be linear elastic (general isotropic fourth-order Hooke's law for continuous media) or viscoelastic (memory variables method). More...
subroutine, public	compute_absorption_forces ()
	This subroutine computes absorption forces \( \int _{\Gamma} \mathbf{v} ^{T} \cdot \mathbf{T} \, d\Gamma \) for any spectral-elements order. A so-called 'P1' explicit paraxial formulation is used to approximate the traction.
subroutine, public	compute_external_force ()
	This subroutine sets external forces \( F^{ext} \) of the system \( M\ddot{U} + C\dot{U} + KU = F^{ext} \) for double couple and single force point sources. More...

Detailed Description

Definition at line 127 of file module_solver.f90.

Member Function/Subroutine Documentation

subroutine, public mod_solver::compute_external_force

(

)

Returns

: filled external force vector : see global variable mod_global_variables::rg_gll_acceleration

Definition at line 1608 of file module_solver.f90.

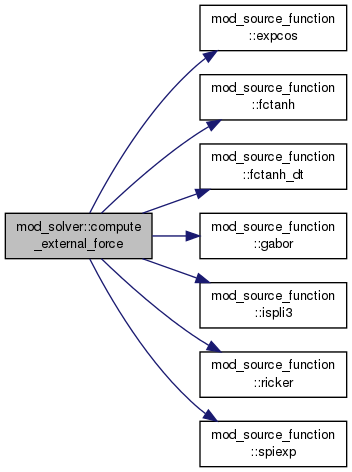
References mod_source_function::expcos(), mod_source_function::fctanh(), mod_source_function::fctanh_dt(), mod_source_function::gabor(), mod_source_function::ispli3(), mod_source_function::ricker(), and mod_source_function::spiexp().

Referenced by efispec3d().

Here is the call graph for this function:

subroutine, public mod_solver::compute_internal_forces_order4	(	integer, intent(in)	elt_start,
		integer, intent(in)	elt_end
	)

Parameters

elt_start	: first hexahedron element of the loop
elt_end	: last hexahedron element of the loop

Definition at line 245 of file module_solver.f90.

Referenced by efispec3d().

subroutine, public mod_solver::compute_internal_forces_order5	(	integer, intent(in)	elt_start,
		integer, intent(in)	elt_end
	)

Parameters

elt_start	: first hexahedron element of the loop
elt_end	: last hexahedron element of the loop

Definition at line 648 of file module_solver.f90.

Referenced by efispec3d().

subroutine, public mod_solver::compute_internal_forces_order6	(	integer, intent(in)	elt_start,
		integer, intent(in)	elt_end
	)

Parameters

elt_start	: first hexahedron element of the loop
elt_end	: last hexahedron element of the loop

Definition at line 1082 of file module_solver.f90.

Referenced by efispec3d().

subroutine, public mod_solver::newmark_end

(

)

Returns

accelerations at step n+1 : see global variable mod_global_variables::rg_gll_acceleration

velocities at step n+1 : see global variable mod_global_variables::rg_gll_velocity

Definition at line 204 of file module_solver.f90.

Referenced by efispec3d().

subroutine, public mod_solver::newmark_ini

(

)

Returns

displacements at step n+1 : see global variable mod_global_variables::rg_gll_displacement

velocities at step n+1/2 : see global variable mod_global_variables::rg_gll_velocity

external forces flush to zero : see global variable mod_global_variables::rg_gll_acceleration

Definition at line 150 of file module_solver.f90.

Referenced by efispec3d().

---

The documentation for this module was generated from the following file:

• module_solver.f90